数学において、そんな経験はありませんか?
苦手分野が足を引っ張ってしまう…。
方程式は得意なのに、確率の問題は苦手。
関数の問題は得意なのに、空間図形の問題は苦手。
特定の分野の問題だけ、極端に点数を落としてしまい、
何とか対策として問題演習を重ねているけど、それでも点が伸びない。
定期テストや宮崎県高校入試において、出題範囲が決まっている以上、
弱点分野を克服しないまま試験に挑むという事は、そのまま確実な減点へと繋がってしまいます。
そんな悩めるあなたに、最高級のアドバイスをします!
弱点分野を克服する上で最も大切なのは、
1つでも多くの『解法パターンの引き出し』を準備する事です。
それでは、詳しく説明してきましょう。
反復学習で解法パターンを身に付ける
数学において、同じ問題を繰り返して解くという事には、
あまり意味を見出せないと考える人もいるかもしれません。
しかし実際は、解法パターンが頭に定着しているかどうかを確認する上で、
とても有意義な勉強となります。
答えが正しいかどうかに焦点を置くのではなく、
解き方を理解しているかという視点で演習する事が大切なのです。
例えば、以下のような因数分解の問題が並んでいたとします。
- X2-8X+12
- X2+10X+25
- X2-16
- X2+14X+49
- X2-81
- X2-9X-52
この6問を順番に解いて、正解か不正解かを確認するという作業で終わらせるのではなく、
丸付けをする前に必ず、それぞれの問題でどんな『解法パターン』を採用したのか分析してください。
①と⑥は、3つ目の項の約数から、(X+A)(X+B)の形を目指す(いわゆる、基本的なタスキがけ)
②と④は、10(2×5)と25(52)、14(2×7)と49(72)という数字から、(X+A) 2の形を目指す
③と⑤は、-16(-42)、-81(-92)という数字から、(X+A)(X-A)の形を目指す
上記のように、それぞれの問題でどの『解法パターン』を使ったかを完璧に説明できれば、
その『解法パターン』が身についているという事の証明になります。

ここで思い出してほしいのは、皆さんが学校や教科書で解いている問題です。
解き方の説明を受けた直後で、それを使って解く問題に挑む機会が多いと思います。
直前で習った解き方で問題を解くせいで、自然と正解率が上昇して、
つい分かった気になってしまうという現象が起こりやすいのです。
このような勘違いを防ぐ上でも、反復復習で理解度を図るのは重要でしょう。
同じ問題で過去に正解したからと言って、決して蔑ろにせず、
『解法パターン』の定着を確認するために、是非とも反復学習に取り組んでください!
そして、できるだけ様々な『解法パターン』がランダムに混在している問題を
積極的に解くような勉強も意識してくださいね!
同類の問題で解法パターンを身に付ける
まず、こちらをご覧ください。
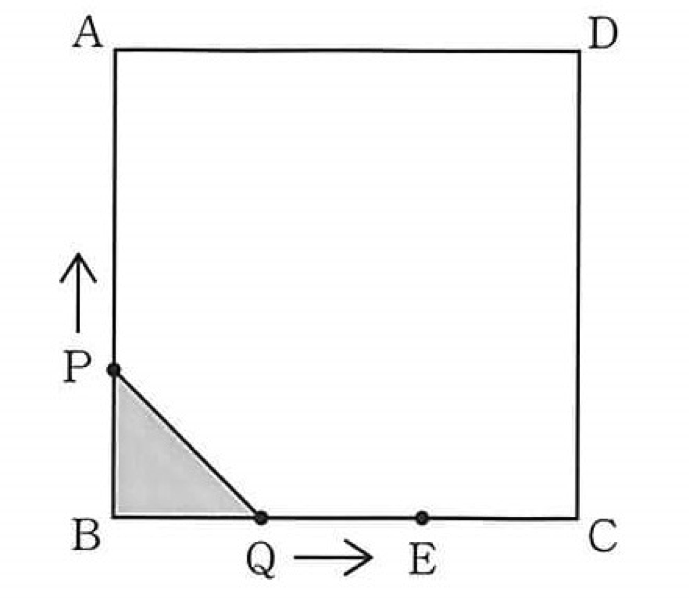
問題文は省きましたが、2020年度の宮崎県公立入試で出題された問題に登場する図です。
それでは次に、こちらをご覧ください。
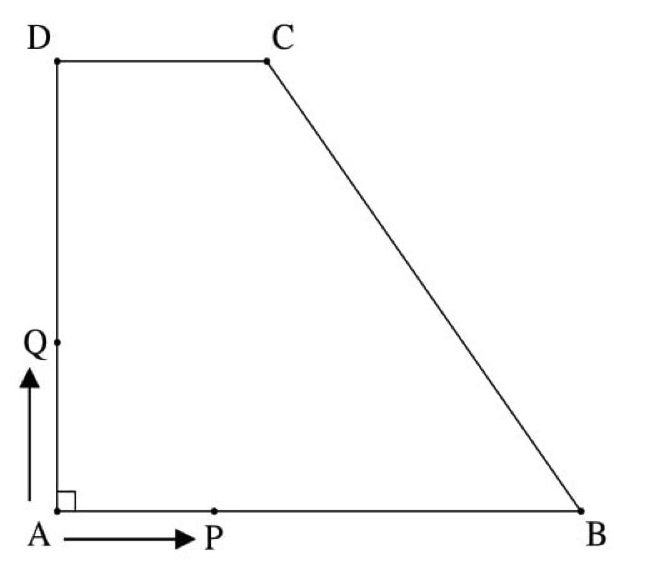
これは、2021年度の埼玉県公立入試で出題された問題に登場する図です。
どちらも点P点Qが登場し、どちらも毎秒1cmで辺を移動し、
どちらも点PとQが頂点の三角形の面積が問題に絡んでくるなど、
2つの問題には多くの共通点があります。
このように、異なる都道府県の公立入試で似た形式の問題が登場する事があります。
実際、図形上の動点P、Qを用いた関数の問題というのは、よくあるパターンの問題です。
しかし、まるっきり同じ問題という事にはならないので、
自分が習得した同類の『解法パターン』を再現できるかどうかが肝心となります。
だからこそ、出会う問題1つ1つの分析を心がけて、
『解法パターン』を正しく分類する事がとても大切なのです。
解き方が分からなかった問題に出会った時に、そこで学習を終わらせず、
意図的に同類の問題を選別して、『解法パターン』を確立していく。
それをノートにまとめて、自分だけの『解法パターン』戦略ノートを作成する。
このような積み重ねで、1つ1つ『解法パターン』の引き出しを増やせば、
受験やテストで出会う問題全てが「新出問題」ではなく「類題」となる可能性が非常に高まります。

問題を見た瞬間に「既視感(なんか見たことある問題だなという感覚)」を覚えたあなたは、
これは前に解いたあの問題と似ているから、あの解法が使えるかも!
という思考に至り、
あらゆる問題に対応しやすくなって、より正解を導けるようになるのです!
最後に
さて、『解法パターン』を身に付ける重要性が、理解できたでしょうか?
難しい問題に直面した時に、最初から無理だと投げ出そうとせず、
過去の経験、今まで積み重ねた数々の問題演習を生かして解くんだ!
という姿勢を持ってください。
特に苦手な分野において、問題の解き方を0から探るのは苦難の道なので、
『解法パターン』通りに形式的に解くというレールを敷くだけでも、
問題の解き始めをサポートしてくれるでしょう。
臨機応変に色んな問題に対応できる柔軟性を手に入れるためにも、
是非とも今日から『解法パターンの引き出し』作りに取り掛かってみてくださいね!
面白いくらいに成績が伸びました!!
「嫌われる勇気」で有名なアドラーの考え方を教育の現場に取り入れたら…
「子供が自ら動き出しました!」
「勉強へのやる気が一気に上がりました!」
「面白いくらい成績が伸びました!」
こんな声が次々に飛んできて、自分でも驚きました!
そんな、お家でも実践できる方法をまとめた塾長の書籍をAmazonで販売中です。
実は、ホームページに訪れていただいた方だけに・・・
期間限定で870円→0円でプレゼントしています!
(下記のLINEにご登録ください。1分以内にメッセージに届きます。)
(無料体験授業も実施中です)
その他
関連記事























